Programación funcional

Programación Funcional

Motivación

Para entender mejor la programación funcional, debemos tener claro que con ella resolvemos a la pregunta ¿Qué? mientras que la programación imperativa responde a la pregunta ¿Cómo?
Al responder la pregunta del “¿Qué?”, nos enfocamos en el resultado y no en el procedimiento. Esto implica un nivel mayor de abstracción, pero también que la programación es independiente del contexto.
Uno de los principios del paradigma es hacer que las funciones sean lo más específicas posible. De esta manera se cumple otro de los principios de este paradigma: la reutilización de código -pues, como veremos, las funciones retornarán lo mismo siempre a lo largo de toda la ejecución del programa-.
La programación funcional se centra en escribir funciones puras, evitando efectos secundarios y utilizando estructuras de datos inmutables. Esto conduce a un código que es más:

Limpio y Legible: Al evitar los efectos secundarios y trabajar con funciones puras, el código se vuelve más predecible y fácil de leer. Esto reduce el riesgo de errores y facilita el mantenimiento.
Modular: La capacidad de componer funciones facilita la creación de componentes pequeños y reutilizables que se pueden combinar para formar aplicaciones más grandes. Esto mejora la modularidad y permite el desarrollo incremental.
Facilita el Testing: Las funciones puras son más fáciles de probar porque su salida depende únicamente de sus entradas, lo que simplifica la creación de pruebas unitarias.
Conciso: La programación funcional permite expresar ideas complejas de manera concisa utilizando características como las expresiones lambda y las funciones de orden superior. Esto reduce la cantidad de código necesario para implementar una funcionalidad.

Este paradigma en ciertos escenarios no solo mejora la calidad del código sino que también aumenta la productividad del desarrollo, ya que permite enfocarse en resolver problemas de negocio sin preocuparse por los detalles de implementación.

Filosofía

Este paradigma de programación tiene dos filosofias principales:

1. Debemos renunciar a compartir estados, mutar datos y pensar en ámbitos locales o globales, en este paradigma lo más importante es pasar argumentos a una función que calculará la salida finalmente.

2. Las funciones son el corazón, este paradigma está compuesto de funciones puras y varias funciones que se unen para crear una función más compleja, para permitir la reutilización y obtener varias combinaciones.

Paradigma Declarativo

La intención es el que se hace, más no el cómo se hace.
Una de las preguntas que todo programador de calidad debe hacerse antes de empezar a trabajar es ¿Que tecnología es la mejor para solucionar este problema? Una pregunta complicada pero que con la respuesta indicada puede facilitar mucho el trabajo, es por ello que usualmente se opta por usar una tecnología con la cual se encuentre familiarizado, es por ello que la programación declarativa no se nos suele pasar por la cabeza, ya que usualmente usamos la programación imperativa.

¿De que se trata la programación declarativa?
En el paradigma de programación declarativa a diferencia del paradigma de programación imperativa el programa se describe en términos de su respuesta, más no en el conjunto de secuencias e instrucciones para llegar a ella, esto puede llegar a ser complicado debido a que usualmente los algoritmos programados se realizan en torno a los pasos para la solución de un problema específico, pero para el paradigma declarativo es más importante tener bien definido un conjunto de condiciones, proposiciones, afirmaciones, restricciones, ecuaciones o transformaciones las cuales modelan la solución al problema en cuestión.

Declarativo

Control del programador es nulo en la secuencia del programa
Se enfoca en el que
Lista como estructura fundamental
No hay asignación destructiva
Solo existen valores y expresiones matemáticas que generan nuevos valores desde los ya declarados
El control no es responsabilidad del programador

Imperativo

El programador tiene control sobre la secuencia del programa
Se enfoca en el cómo
Se fija en como realizar operaciones ayudándose de patrones de control de flujo
Asignación destructiva
Presenta efectos colaterales
El control por parte del programador es excesivo

Historia

Todo empiezó con Gottfried Leibniz, quien creó la máquina mecánica de cálculo en el siglo XVII. Esta máquina fue el primer prototipo del dispositivo soñado por Leibniz: una máquina capaz de manipular símbolos y determinar si una frase matemática era o no un teorema, es decir, si una proposición que partía de un supuesto (hipótesis), afirmaba una verdad (tesis) que no es evidente por sí misma.

Para el año de 1928, los matemáticos David Hilbert y Wilhelm Ackermann propusieron el problema de la decisión, que consiste en encontrar un proceso o algoritmo (aún no se tenía la definición formal de algoritmo como tal) general, que decidiera si una fórmula de cálculo de primer orden es un teorema retomando la idea desarrollada por Leibniz.

En 1936, Alonzo Church desarrolló la definición formal de algoritmo bajo el concepto de “calculabilidad efectiva” y diseñó una solución al problema planteado por Hilbert y Ackermann utilizando un modelo de computación denominado por él mismo como Cálculo Lambda, la base fundamental de este paradigma.

En este mismo año, Alan Turing -al igual que Church- desarrollaba una definición de algoritmo y daba solución al problema de la decisión, pero usando las máquinas de Turing, otro modelo de computación que se convertiría en la base de la computación actual, bajo un concepto completamente diferente al cálculo lambda: el problema de la parada. Cabe aclarar que los dos modelos computacionales son equivalentes ya que ambos pueden dar solución a los mismos tipos de problemas. Cabe destacar que la solución de Turing se basa en un modelo computacional basado en estados, esto dada su definición formal que usa un "estado interno" para representar el estado de una ejecución. Por otro lado, Church dio una solución desde el punto de vista de como se computan las funciones, donde no tiene sentido un estado interno ni nada que no sea puramente una función.

El paradigma funcional se empezó a desarrollar por el matemático John McCarthy en 1956, para programar los primeros proyectos de inteligencia artificial sobre un computador IBM 704 durante su desarrollo este crea el lenguaje de programación lisp en 1958.

Lisp fue creado originalmente como una notación matemática práctica para los programas de computadora, basada en el cálculo lambda de Alonzo Church. A pesar de no ser un lenguaje puramente funcional Se convirtió rápidamente un lenguaje de programación pionero en la investigación de la inteligencia artificial (AI) estableciendo las bases de lo que se conocería hoy como el paradigma funcional

Cálculo Lambda

Es el más pequeño lenguaje universal de programación, consiste en en una regla de transformación simple (sustituir variables) y un esquema simple para definir funciones.

El cálculo lambda se puede decir que es equivalente a las máquinas Turing porque es capaz de evaluar y expresar cualquier función computable. Originalmente, Church había tratado de construir un sistema formal completo para modelar la Matemática; pero cuando éste se volvió susceptible a la paradoja de Russell, separó del sistema al cálculo lambda y lo usó para estudiar la computabilidad, culminando en la respuesta negativa al problema de la parada.

Es un sistema formal que utiliza la abstracción del concepto de función desde un punto de vista computacional. Esta consiste de 3 simples reglas:

El uso de variables que representan funciones o valores matemático-lógicos. [x]
Definición de funciones como términos Lambda. [(λx.M)]
Aplicación de funciones. Dados términos consecutivos, el primero es una función que toma como parámetros los valores necesarios a su derecha, de acuerdo a su definición. (M N)

Estas reglas se pueden evidenciar de la siguiente manera:

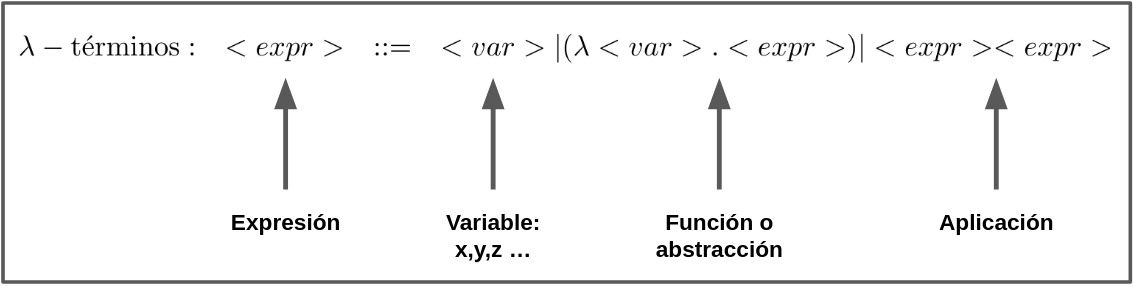
Cada una de las partes de la expresión tiene un respectivo significado:

Variables: Son la representación abstracta de un objeto, se pueden nombrar con distintas letras.

Abstracción o función: Es la definición de una función donde:

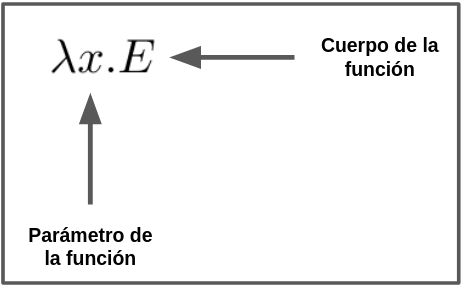
Como las funciones pueden tener una expresión como cuerpo, la siguiente sería una expresión válida:

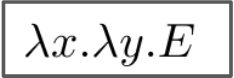
Debido a que en el cálculo lambda formal una función solamente pueden recibir un único parámetro, es necesario utilizar la currificación. El ejemplo anterior evidencia como una función con un parámetro X, tiene como cuerpo otra función con parámetro Y, la cual tiene como cuerpo una expresión E.

Aplicación: Una expresión seguida de otra.

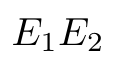
Uno de los aspectos fundamentales del cálculo lambda es la (β-reducción).

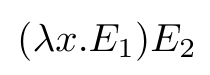
Al aplicar (β-reducción), se reemplazan las apariciones libres de X en el cuerpo E1 con la expresión E2.

Ejemplo de β-reducción utilizando cálculo lambda formal:

El siguiente ejemplo muestra cómo realizar la suma de dos números utilizando cálculo lambda.

Suponga que tenemos la función f(x,y) = x+y, a continuación se muestra un gráfico que representa las entradas de la función y la respectiva salida.

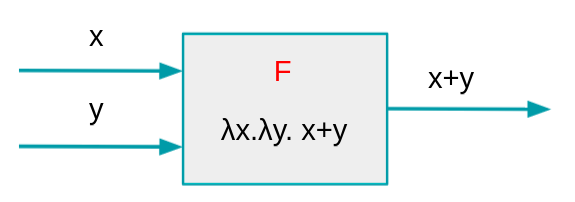
Se puede evidenciar como hay 2 funciones, la más externa recibe X como parámetro y tiene como cuerpo otra función que recibe Y como parámetro, el cuerpo de esta función interna es X+Y. Se va a realizar β-reducción con los parámetros 4 y 2. Se empieza resolviendo la función que esté más a la izquierda, para esto se reemplaza cada aparición de X en el cuerpo de la función con 4. Una vez reducida esa función, se realiza el mismo procedimiento con el otro parámetro.

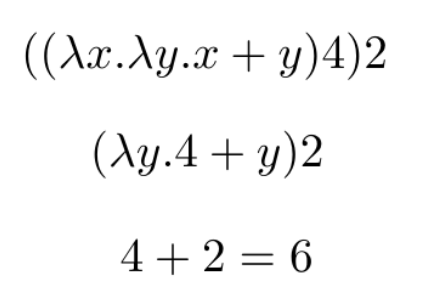
El resultado final de reducir la expresión es 4+2 obteniendo como resultado 6.

Con estas simples reglas se pueden formular los operadores lógicos más básicos, como se muestra a continuación:

TRUE = λx. λy. x

FALSE = λx. λy. y

NOT = λb. b TRUE FALSE

AND = λx. λy. x y FALSE

OR = λx. λy. x TRUE y

Considérese las siguientes dos funciones. Por un lado, la función identidad I(x)=xI(x)=x, que toma un único argumento, xx, e inmediatamente devuelve xx. Por otro lado, la función suma S(x,y)=x+yS(x,y)=x+y, que toma dos argumentos, xx e yy, y devuelve la suma de ambos: x+yx+y, usando estas dos funciones como ejemplo podemos decir:

Teoría de Categorías

La teoría de categorías es una rama de las matemáticas que cambió la forma en que vemos y entendemos las estructuras matemáticas. Fue creada por los matemáticos Samuel Eilenberg y Saunders Mac Lane en la década de los 40, y desde entonces ha tenido un gran impacto en diversos campos como la física teórica y la informática. A grandes rasgos, esta teoría intenta axiomatizar muchas de las estructuras matemáticas generalizándolas en una sola, centrándose en las relaciones entre ellas más que en su propio significado. Haciendo una analogía, se parece a cuando estamos armando un rompecabezas y en vez de concentrarnos en las piezas específicamente, observamos cómo todas las piezas encajan y se conectan.

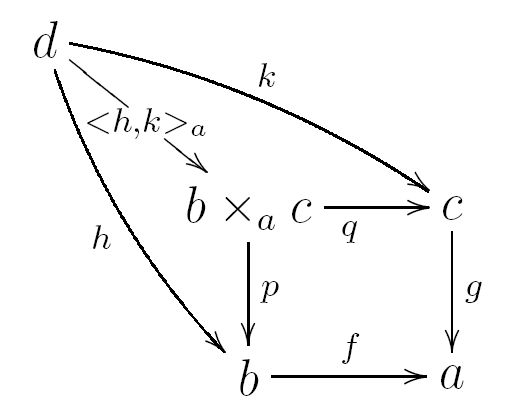
Las categorías en esta teoría pueden verse como mundos matemáticos y los functores hacen las veces de traductores que nos ayudan a entender cómo los elementos de una categoría se relacionan con los elementos de otra, en otras palabras, son puentes que conectan distintas áreas de la matemática. Otro concepto relevante es el de morfismo, este puede interpretarse de una manera general como una función que conecta cualquier par de elementos de una categoría coherentemente. Adicionalmente, esta teoría ha influido en la programación, ayudando al diseño de nuevos lenguajes programación y a la comprensión de la semántica de los programas.

Siguiendo este orden de ideas, la teoría de categorías ha tenido un impacto significativo en la programación funcional ya que esta ofrece un marco sólido para enteder y desarrollar las funciones, las cuales son el pilar fundamental del paradigma, de manera elegante y eficiente. Por ejemplo, la teoría de categorías brinda el formalismo matemático adecuado para enunciar conceptos como el de functor o mónada, los cuales se pueden asociar a las funciones que toman otras funciones como argumentos y retornan nuevas funciones y al método usado por excelencia para manejar efectos secundarios respectivamente. Además, hace que el paradigma se acoja a los estándares de inmutabilidad, funciones puras y la composición de funciones de distinto orden.

Ventajas

Altos niveles de abstracción: El código muestra un mayor énfasis en el "¿qué se hace?" en lugar del "¿cómo se hace?".
Código declarativo y comprensible: Debido a los altos niveles de abstracción, los programas que aplican este paradigma suelen ser más cortos y fáciles de entender que sus versiones en programación imperativa.
La evaluación perezosa: Esta estrategia de evaluación permite realizar cálculos por demanda, evitando gasto computacional innecesario. El ejemplo más claro está en la utilización de listas infinitas. El uso de Lazy Evaluation permite optimizar el tiempo necesario para realizar computaciones. Múltiples plataformas de Big Data, como Apache Spark, hacen uso del paradigma para obtener estos beneficios.
Las características del paradigma, en especial la utilización de funciones puras, permiten realizar ciertas optimizaciones particulares.
Mayor probabilidad de aplicar expansión en línea: Esta es una optimización del compilador que sustituye los llamados a una función por la definición directa de dicha función, de tal forma que se ahorre tiempo y espacio durante la ejecución.
Combinación con otros paradigmas: Por su alto nivel de abstracción, es facil utilizarlo junto a varios paradigmas de programación, ejemplo POO, ya que solo requerimos del uso de funciones puras y de contextos locales.
Las características del paradigma, en especial la utilización de funciones puras, permiten realizar ciertas optimizaciones particulares.
Optimizaciones a partir de la utilización de funciones puras: Las funciones puras nos garantizan la ausencia de efectos secundarios. Esto a su vez nos permite aplicar las siguientes mejoras:
- Se pueden eliminar las funciones cuyo resultado no sea utilizado.
- Una función retornará lo mismo siempre que se ejecute con los mismos parámetros, por lo cuál se puede evitar la repetición de cálculos mediante el uso de memoria caché.
- El orden de ejecución de las funciones puede ser cambiado o incluso se puede llegar a aplicar paralelismo cuando no exista dependencia de datos entre dichas funciones.

Desventajas

Dificultad inicial para producir buen código: Esto debido a que un programador suele estar acostumbrado al pensamiento de la programación imperativa, tomando un poco de tiempo que la persona logre adaptarse y generar código útil. No solo eso, sino que la terminología incluida dentro de la programación funcional (combinator, monoid, monad, functor) puede ser intimidante cuando se inicia desde una base de programación netamente imperativa. Y puede ser aún peor cuando no se posee experiencia en el tema.
Generación de grandes cantidades de short-lived garbage: Esto se debe principalmente a la característica de inmutabilidad. Los garbage collectors tienden a optimizar este aspecto.
Menos útil en situaciones que requieren cambio de estado frecuente, si requerimos llevar un control global de un estado o una variable, esto es complicado, requerira adaptar el codigo de otra manera y hacer uso, varias veces, de la composición de funciones, durante toda la ejecucción de nuestro codigo. La programación funcional puede ser menos eficiente en algunos casos en comparación con otros paradigmas de programación. Esto se debe a que la programación funcional se enfoca en la evaluación de expresiones y funciones matemáticas, lo que puede requerir más tiempo de procesamiento y más recursos de memoria en algunos casos.
Menor eficiencia en el uso de CPU comparados con su contraparte imperativa: Debido principalmente a que muchas estructuras de variables mutables (como los arreglos) tienen una sencilla implementación en un paradigma imperativo, mientras que en la programación funcional no es fácil crear componentes homólogos inmutables con la misma eficiencia.
El uso de I/O (Archivos, Bases de datos y GUIs) se vuelve un problema. La manipulación de estas entradas y salidas requiere de funciones netamente impuras. Un programa que provea utilidad al usuario necesitará, en la gran mayoría de casos, acceso a este tipo de entradas y salidas.

Ventajas técnicas

Ventajas relacionadas con el uso de lenguajes funcionales o fáciles de implementar debido a sus principios aplicados en estos

Expresividad

Dado que la programación funcional simplifica el código de manera significativa el uso de esta facilita en gran manera la definición de las estructuras globales lo que permite un mayor entendimiento de estas un ejemplo de esto es el uso de los datos algebraicos en haskell que son aquellos que nos permiten el uso de argumentos como constructores una extensión de las funciones de orden superior usadas en este paradigma.

Pruebas Unitarias

La programación funcional se destaca en las pruebas unitarias gracias a su énfasis en las funciones puras, las cuales carecen de efectos secundarios y dependencias externas, lo que facilita la creación de pruebas aisladas y predecibles. Al ser inmutables y reproducibles, las funciones puras permiten simular diversas entradas sin corromper los datos, fomentando así una composición modular y una sustitución sencilla en el proceso de prueba. Esta naturaleza simplifica la identificación y corrección de errores, garantizando un desarrollo de software más confiable y eficiente. Es comun usar la programación funcional en metodologias orientadas a los test como el Test-Driven Development(TDD).

Seguridad

Inmutabilidad: Característica existente en los lenguajes funcionales en la cual que un objeto no puede cambiar su estado. Como consecuencia, esta característica aporta muchas facilidades al momento de razonar sobre el código que estemos creando, y a que no tenemos que preocuparnos por cambios que puedan sufrir los objetos a lo largo del programa. Como ventaja adicional, los objetos que son inmutables, se vuelven automáticamente seguros en el manejo de hilos (o thread-safe) de manera en que pueden ser accedidos de manera concurrente sin presentar ningún tipo de "side effects" debido a que no pueden modificarse. Manejo de errores:Debido a la característica principal de este paradigma (programar mediante funciones),Es relativamente mas fácil detectar errores en el código, ya que al separarlo por funciones, no es necesario revisar todo el código como habría que hacerlo si se hubiera programado de forma imperativa.

Paralelismo

La programación funcional se caracteriza por la ausencia de cambios en estados globales, lo que permite "ignorar" el tiempo en un sentido particular. Esto significa que podemos dejar de preocuparnos por el momento en que las funciones acceden a una variable compartida, lo que podría dar lugar a resultados variables. Al evitar la mutabilidad de las variables, eliminamos la necesidad de rastrear cuándo y cómo se accede a ellas, obteniendo respuestas consistentes según la lógica de programación. En el contexto de la programación paralela y concurrente, estas preocupaciones suelen requerir estructuras y técnicas de sincronización complejas, como cerraduras, semáforos, funciones y variables atómicas, variables de condición, monitores, etc.

Sin embargo, la programación funcional se convierte en una solución eficaz para lograr el paralelismo al proporcionar un enfoque más limpio y claro. A pesar de sus limitaciones, la programación funcional se muestra como una herramienta poderosa para la concurrencia, pues ofrece ventajas notables, como la programación declarativa, que se basa en expresar lo que se quiere hacer en lugar de cómo hacerlo. Esto permite a los sistemas de concurrencia tomar decisiones más eficientes sobre cómo ejecutar tareas en paralelo, ya que se pueden reorganizar y optimizar las operaciones sin cambiar el resultado final. La evaluación perezosa, otra ventaja, significa que las expresiones no se evalúan hasta que sea necesario, lo que mejora la eficiencia en situaciones de concurrencia al evitar cálculos innecesarios.

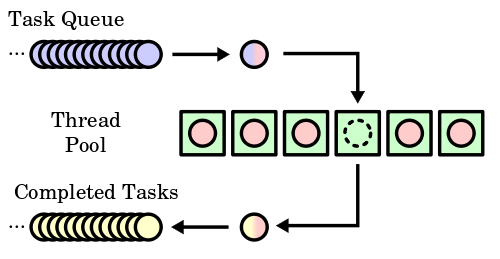
La programación funcional, además de promover la composición de funciones, lo que facilita la construcción de sistemas concurrentes a partir de componentes pequeños y reutilizables, sobresale en la inferencia de dependencias. En un paradigma funcional, las dependencias entre funciones se vuelven más claras y explícitas, lo que simplifica la identificación de tareas que pueden ejecutarse en paralelo sin preocupaciones por problemas de dependencias. Este enfoque funcional también aboga por el aislamiento de estado, lo que implica que las secciones del programa no comparten datos mutables. Esto no solo reduce la probabilidad de condiciones de carrera y otros problemas comunes en la concurrencia, sino que también mejora la seguridad general. Las funciones puras, inherentes a la programación funcional, garantizan que múltiples procesos concurrentes nunca intenten acceder simultáneamente a los mismos datos, eliminando así una de las preocupaciones más desafiantes en la concurrencia, conocida como condiciones de carrera. En resumen, la programación funcional ofrece un enfoque altamente efectivo para abordar la concurrencia al eliminar las inquietudes sobre la compartición de estados y al permitir un diseño más seguro, eficiente y mantenible de sistemas concurrentes.

Lenguajes de programación

A continuación se mencionarán y se dará una breve introducción con algunos ejemplos de lenguajes que implementan características del paradigma de programación funcional:

SCALA

Es un lenguaje de programación multi-paradigma diseñado para expresar patrones comunes de programación que integra características de lenguajes funcionales y orientados a objetos. La implementación actual corre en la máquina virtual de Java y es compatible con las aplicaciones Java existentes. En Scala las funciones son valores de primera clase, soportando funciones anónimas, orden superior, funciones anidadas y currificación. Scala viene integrado de fábrica con la técnica de pattern matching para modelar tipos algebraicos usados en muchos lenguajes funcionales. El siguiente código muestra una de las características de la programación funcional, el pasar funciones como argumentos de otras funciones.

SCHEME

Es un lenguaje funcional (si bien impuro pues sus estructuras de datos no son inmutables) y un dialecto de Lisp. Fue desarrollado por Guy L. Steele y Gerald Jay Sussman en la década de los setenta e introducido en el mundo académico a través de una serie de artículos conocidos como los Lambda Papers de Sussman y Steele. La filosofía de Scheme es minimalista. Su objetivo no es acumular un gran número de funcionalidades, sino evitar las debilidades y restricciones que hacen necesaria su adición. Así, Scheme proporciona el mínimo número posible de nociones primitivas, construyendo todo lo demás a partir de un reducido número de abstracciones. Las listas son la estructura de datos básica del lenguaje, que también ofrece arrays entre sus tipos predefinidos. Debido a su especificación minimalista, no hay sintaxis explícita para crear registros o estructuras, o para programación orientada a objetos, pero muchas implementaciones ofrecen dichas funcionalidades. El siguiente ejemplo muestra porque Scheme es un lenguaje funcional impuro, permitiendo realizar estructuras como for, las cuales incumplen la regla de que los objetos son inmutables.

Haskell

Es un lenguaje de programación estandarizado multi-propósito puramente funcional con semánticas no estrictas y fuerte tipificación estática. Su nombre se debe al lógico estadounidense Haskell Curry. En Haskell, "una función es un ciudadano de primera clase" del lenguaje de programación. Como lenguaje de programación funcional, el constructor de controles primario es la función. El lenguaje tiene sus orígenes en las observaciones de Haskell Curry y sus descendientes intelectuales. Las características más interesantes de Haskell incluyen el soporte para tipos de datos y funciones recursivas, listas, tuplas, guardas y calce de patrones.

ERLANG

Erlang es un lenguaje de programación altamente funcional y concurrente, diseñado para construir sistemas robustos y escalables en entornos de telecomunicaciones y aplicaciones distribuidas. Sus propiedades funcionales se centran en la inmutabilidad de datos, la ausencia de efectos secundarios y la concurrencia basada en actores. En Erlang, los procesos son entidades ligeras que se comunican a través de mensajes, permitiendo una alta concurrencia y una arquitectura resistente a fallos. Además, Erlang promueve el uso de patrones funcionales, como la recursión y el patrón "head-tail," lo que hace que el código sea más claro y mantenible. Su énfasis en la tolerancia a fallos y la escalabilidad lo convierte en una herramienta poderosa para aplicaciones distribuidas y sistemas en tiempo real.

Lisp

Lisp, acrónimo de "List Processing," es un lenguaje de programación de alto nivel que se destaca por su rica historia en el ámbito de la programación funcional. Una de las características distintivas de Lisp es su representación de datos y código en forma de listas, lo que lo convierte en un lenguaje muy flexible y expresivo. Proporciona un ambiente propicio para la programación funcional debido a su énfasis en funciones de orden superior, donde las funciones pueden tratarse como datos y pasarse como argumentos. Lisp también promueve la recursión como una técnica fundamental y fomenta la creación de funciones puras que evitan efectos secundarios. Su enfoque en la inmutabilidad de datos y la facilidad de creación de nuevas funciones lo convierte en un lenguaje adecuado para la construcción de software confiable y mantenible. Lisp ha influido en el desarrollo de otros lenguajes funcionales y sigue siendo relevante en campos como la inteligencia artificial y la programación simbólica.

Idris

Idris es un lenguaje de programación funcional y dependiente de tipos que se destaca por su sistema de tipos fuerte y flexible, permitiendo a los programadores especificar tipos de datos de manera precisa y demostrar propiedades de programas a través de teoremas y pruebas formales. Con características como evaluación perezosa, pattern matching, efectos y metaprogramación, Idris ofrece un enfoque versátil para la escritura de software confiable y verificable. Su comunidad activa y creciente biblioteca estándar lo convierten en una opción atractiva para aquellos que buscan un lenguaje de programación que combine los principios funcionales con una sólida verificación de tipos.

ELM

Elm es un lenguaje de programación funcional puro diseñado para el desarrollo de aplicaciones web front-end. Una de sus características distintivas es su fuerte énfasis en la arquitectura de la aplicación, siguiendo el patrón Modelo-Vista-Actualización (Model-View-Update, MVU). Elm está diseñado para garantizar la ausencia de errores en tiempo de ejecución al eliminar efectivamente los problemas de acceso a nulos, excepciones y otros errores comunes en el desarrollo web. Con un sistema de tipos sólido y una sintaxis simple, ELM promueve la legibilidad y la mantenibilidad del código, lo que lo hace una elección popular para proyectos front-end donde la estabilidad y la seguridad son fundamentales. La comunidad de Elm también es conocida por su enfoque en la documentación y la promoción de mejores prácticas de programación en el desarrollo web.

CLOJURE

Es un lenguaje de programación de propósito general que maneja el dialecto de Lisp, está enfocado en el paradigma funcional y fue diseñado con el fin de eliminar la complejidad de la programación concurrente, se puede ejecutar sobre la máquina virtual de Java, la máquina de la de la plataforma .NET o compilado a JavaScript. Este lenguaje usa una gestión de referencias que pueden ser actualizadas aplicando funciones pras al estado actual, permitiendo un enfoque al cambio de estado de la programación imperativa promoviendo el uso de funciones puras como mejor forma de realizar cálculos. Fue diseñado por Rich Hickey, quien describe el desarrollo de Clojure como la búsqueda de un lenguaje funcional como el Lisp, pero por defecto, que estuviera integrado sobre un entorno robusto en lugar de ser su propia plataforma y que eliminara la programación concurrente. Así mismo rechaza por completo el paradigma de los objetos, expresando los programas como aplicación de funciones sobre datos mas que sobre interaccion e entidades.

OCaml

Objective CAML, su etimología proviene de las siglas Objective Categorical Abstract Machine Language. Es un lenguaje de programación avanzado de la familia ML, desarrollado por INRIA en Francia, admite varios paradigmas, entre ellos el funcional. Nace de la evolución del del lenguaje CAML, al integrarse la operación con objetos. El código en Ocalm, se compila en código para una máquina virtual o en código de máquina para diferentes arquitecturas que permiten una eficiencia comparable con la producida por lenguajes como C o C++.

JavaScript

Si bien JavaScript no es un lenguaje funcional puro, por medio del uso de algunos conceptos, prácticas y librerías que nos permiten emplear este paradigma:

Asegurar inmutabilidad de los datos con los que trabaja tu aplicación.
Uso de funciones de orden superior.
Uso del currying.
Composición de funciones.

JavaScript permite la declaración de funciones puras muy fácilmente por medio del comando function. Las funciones de orden superior map, filter y reduce, son los pilares de la programación funcional en JavaScript. La composición de funciones es muy similar al manejo de java, con la notación punto.

La programación funcional en JavaScript es muy util pues previene la creación de efectos colaterales en los datos de las aplicaciones. Programación funcional en JavaScript

JAVA 8+

Java es un lenguaje multiparadigma creado por Sun Microsystems (comprada luego por Oracle) en 1991.

En marzo de 2014, es lanzada la versión Java SE 8 la cual incluye expresiones Lambda, añadiendo así funcionalidad de programación funcional.

Kotlin

Es un lenguaje de programación de tipado estático, el cual corre sobre la máquina virtual de Java y también puede ser compilado a código fuente de JavaScript. Fue principalmente desarrollado por JetBrains en sus oficinas en San Petersburgo. Su nombre proviene de una isla llamada Kotlin ubicada cerca a San Petersburgo.

Este lenguaje permite realizar programación funcional debido a que cuenta con inferencia de tipo, permite trabajar con funciones de alto orden y con funciones como ciudadanos de primera clase.

PYTHON

Python es un lenguaje de programación potente y fácil de aprender. Tiene estructuras de datos de alto nivel eficientes y un simple pero efectivo sistema de programación orientado a objetos. La elegante sintaxis de Python y su tipado dinámico, junto a su naturaleza interpretada, lo convierten en un lenguaje ideal para scripting y desarrollo rápido de aplicaciones en muchas áreas para la mayoría de plataformas. El ejemplo a continuación ilustra el uso de maps en lugar de iteradores para aplicar funciones a conjuntos de datos.